程序員必知8大排序3大查找教程（2）

三種查找算法:順序查找，二分法查找（折半查找），分塊查找，散列表（以后談）

一、順序查找的基本思想：

從表的一端開始，順序掃描表，依次將掃描到的結點關鍵字和給定值（假定為a）相比較，若當前結點關鍵字與a相等，則查找成功；若掃描結束后，仍未找到關鍵字等于a的結點，則查找失敗。

說白了就是，從頭到尾，一個一個地比，找著相同的就成功，找不到就失敗。很明顯的缺點就是查找效率低。

適用于線性表的順序存儲結構和鏈式存儲結構。

計算平均查找長度。

例如上表，查找1，需要1次，查找2需要2次，依次往下推，可知查找16需要16次，

可以看出，我們只要將這些查找次數求和（我們初中學的，上底加下底乘以高除以2），然后除以結點數，即為平均查找長度。

設n=節點數

平均查找長度=（n+1）/2

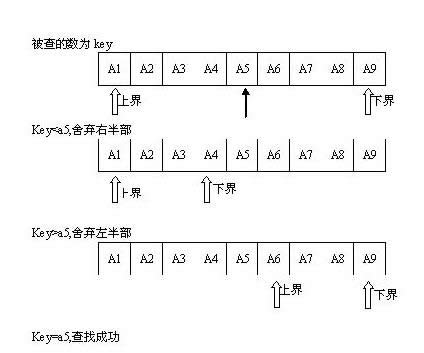
二、二分法查找（折半查找）的基本思想：

前提：

（1）確定該區間的中點位置：mid=（low+high）/2

min代表區間中間的結點的位置，low代表區間最左結點位置，high代表區間最右結點位置

（2）將待查a值與結點mid的關鍵字（下面用R[mid].key）比較，若相等，則查找成功，否則確定新的查找區間：

如果R[mid].key>a，則由表的有序性可知，R[mid].key右側的值都大于a，所以等于a的關鍵字如果存在，必然在R[mid].key左邊的表中。這時high=mid-1

如果R[mid].key<>< span="">則等于a的關鍵字如果存在，必然在R[mid].key右邊的表中。這時low=mid<>

如果R[mid].key=a，則查找成功。

（3）下一次查找針對新的查找區間，重復步驟（1）和（2）

（4）在查找過程中，low逐步增加，high逐步減少，如果high<>< span="">，則查找失敗。<>

平均查找長度=Log2(n+1)-1

注：雖然二分法查找的效率高，但是要將表按關鍵字排序。而排序本身是一種很費時的運算，所以二分法比較適用于順序存儲結構。為保持表的有序性，在順序結構中插入和刪除都必須移動大量的結點。因此，二分查找特別適用于那種一經建立就很少改動而又經常需要查找的線性表。

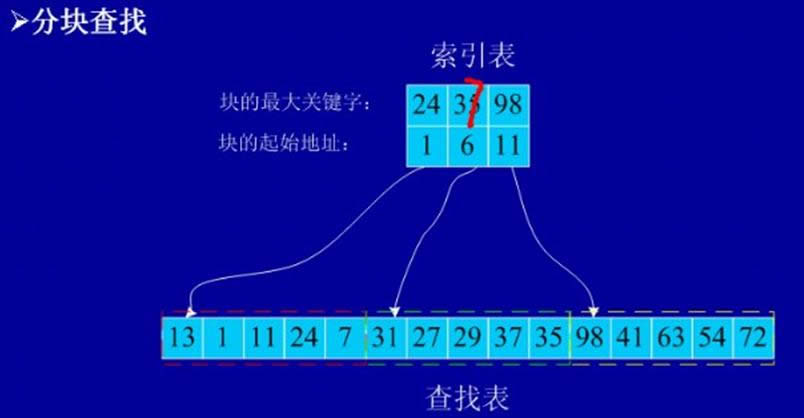
三、分塊查找的基本思想：

二分查找表使分塊有序的線性表和索引表（抽取各塊中的最大關鍵字及其起始位置構成索引表

）組成，由于表是分塊有序的，所以索引表是一個遞增有序表，因此采用順序或二分查找索引表，以確定待查結點在哪一塊，由于塊內無序，只能用順序查找。

設表共n個結點，分b塊，s=n/b

(分塊查找索引表)平均查找長度=Log2（n/s+1）+s/2

(順序查找索引表)平均查找長度=(S2+2S+n)/(2S)

注：分塊查找的優點是在表中插入或刪除一個記錄時，只要找到該記錄所屬塊，就在該塊中進行插入或刪除運算（因塊內無序，所以不需要大量移動記錄）。它主要代價是增加一個輔助數組的存儲控件和將初始表分塊排序的運算。

它的性能介于順序查找和二分查找之間。

四、在理想情況下，無須任何比較就可以找到待查關鍵字，查找的期望時間為O(1)。散列表查找技術不同于順序查找、二分查找、分塊查找。它不以關鍵字的比較為基本操作，采用直接尋址技術。

希望我的這個大家有所幫助，記得在這篇日志下面或者主頁的留言板中留下你們的建議和反饋，這些對我們是最寶貴的財富，預祝大家快樂！有問題大家積極回帖討論下哈！